
The above graph is the quadrupole gravity potential for a rotating sphere drawn along the rotation axis z. Newtonian potential is not included in the picture. The boundary of the star is where Z=1, -1. The square of the form factor is set at 0.02 and the rotational speed at the surface of the star is set at 0.05c, while M=G=c=R=1.
The length of the jets may be determined by the point where the peak height of the dipole potential meets the ordinary Newtonian gravity far out side of the Z axis when a horizontal line is drawn along the Z axis.
While the peak height of the potential is determined by the rotational frequency and the mass of the rotating center and its geometrical shape, there is a mathematical form factor etha that is an arbitrary parameter yet it determines the length of the jets critically. In case of the rotating sphere, however, Lenz-Thirring's result could be used to determine the accurate value of the form factor which turns to be about 0.3R.
In general case, since we do not know exactly how the rotation center may look like in terms of its precise geometrical shape, this arbitrary form factor may be inevitable for the time being.
In actuality, there is little chance that the rotating center will remain like a sphere even if it may have started as one in the beginning. Because of the strong dipole force near the equatorial center, when viewed from the side, it may as well look like two saucers attached together face to face in the horizontal direction.
A slight dimple in the middle of the saucer may define the jet's outlet and the main body spreads out around the equatorial plane which may be much longer than the radius of a typical saucer.
While predictions can be made regarding the length of the jets, other informations obtained from the orbital motion of the galactic system would be critical to determine the validity of its predictions.
http://www.tachyonics.com/NonNewt.pdf
Note: The above Z directional potential is a fixed one to make it consistent with Lens-Thirring force. The actual Z directional potential which is consistent with the dark matter problem should look like,
Friday, April 20, 2007
The Length of the Jets
Radial Dipole Gravity Force in the Equatorial Plane of the Rotation
The radial component of dipole gravity force from the rotating spherical mass in the equatorial plane per unit mass boils down to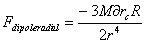
in the range r>>R, where M is the mass and R the radius of the rotating spherical center and delta rc the relativistic center of mass shift for the corresponding hemisphere.
Because of the latitude angular effect, the force has 1/r^4 dependency instead of 1/r^3 as one may expect from the dipole gravity force.
Simple addition of this force to the Newtonian gravity itself may not be enough to explain the velocity curve, however, it must be noted that the matter distribution in the equatorial plane near and around the center will no longer be like a simple Keplerian orbital distribution. It is expected that there will be a lot more of matter distribution in the long stretch of the equatorial plane starting from the center as shown in the following diagram as the rotational speed gets stronger.
Those intermediary matters can not form independent stars because of the excessive gravity forces that prevent them from forming a stable, condensed stellar object.
Dark matters may be just normal matters(baryonic) that can not be visible because they could not be condensed hard and large enough to start the usual stellar thermonuclear fusion process.
As soon as the effect from this fast decreasing 1/r^4 dependent force dies down, in addition to the subsequent reduction of the intermediary matters, the velocity curve will show substantially different path than would be expected from the simple Newtonian gravity.
Thursday, April 19, 2007
Dipole Gravity, Complete Solution for the Dark Matter Problem
In the following we will discuss the dark matter problem within the light of dipole gravity.


{courtesy from Dr.Greg Bothun}
The existence of an additional long range gravity force will certainly help maneuvering the parameters in solving the problems of the dark matter.
However, the radial component of the dipole field strength becomes zero at the 90 degree latitude angle measured from the half of the radius from the top dome of the individual hemisphere due to the cosine dependency of the force through the latitude angle theta, although when the two dipoles are superposed, the equatorial plane of the sphere is not exactly at the location where the latitude angle is 90 degree for both of the dipoles.
And these two contributions to the total radial dipole gravity force is additive rather than subtractive which is a positive sign.
Depending on the physical size of the ultra compact rotating object, there is a region about the size of the radius of the star that the radial component is not zero. It's a matter of detailed calculation if this portion of the radial component of the dipole gravity force in the equatorial plane will be enough to account for the observed anomaly.
A simple form of the radial dipole gravity force in the equatorial plane for r>>R is derived in the link.
A complete solution to the dark matter problem is provided in the link.
"This provides the first direct proof that dark matter must exist and that it must make up the majority of the matter in the Universe." said study leader Doug Clowe, from the University of Arizona.
Extracting Gravitational Energy From the Homogeneous Isotropic Universe
Apart from general relativity and purely from the special relativistic point of view, rotating hemisphere pauses a great mechanical problem in physics, because of its apparent breaking of Newton's second law of motion. Ie, the movement of an object which is a measure of the displacement of its center of mass happens without the corresponding external force in the direction of the displacement.
Of course, this empirical observation was the original cause of the beginning of the quest in this field. If Newton's second law can be broken, it means that the energy conservation law in a local mechanical system can no longer be an absolute physical law.
The paper published in the llnl.gov archive on the title is a result of this research.
Wednesday, April 18, 2007
Alternative Method of Testing Dipole Gravity Effect
In fact, there is an alternative way to detect dipole gravity effect. It is to use the rotating hemispherical rotor itself as a moving projectile. It is not a method of detecting the force directly from the rotor using a probe as a detector. It is rather a method of detecting the force the rotor experiences itself by its interaction with the universe.
This method has several inherent advantages over the other by the fact that even if the force is very small, the long time accumulation of the force can manifest itself in a significant spatial displacement of the rotor.
The size of the rotor doesn't have to be very large. Because of the force law, the displacement will be the same regardless of the size of the rotor, although the force does depend on the rotating speed.
Rotational speed doesn't have to be extremely large, because the effect can manifest accumulatively for a long period of time.
The negative effect from the friction would be insignificant, because of the slowness of the motion at the start and in the following motion.
The key point of this experiment is to mount the rotor on one side of a long balanced arm resting on a pivot, positioned horizontally, in such a way that the axis of rotation is aligned to the tangential direction of the circle of its path and let the force of the nature to turn the arm. In other words, let the hemispherical rotor to work like a horse turning a wheat grinding mill.
It may take weeks or months to notice any displacement of the rotor depending on the force it experiences with the nature. The amount of displacement depends on the square of the time measured in seconds
S=(1/2) a t^2.
Assuming the force on the rotor per unit mass would be in the range of 10^-14 m/sec^2, which is extremely small, the rotor at the end of the arm will still move 5 meters in circle in one year.
Possible errors that may be experienced and need to be dealt with in this experiment will be the rotation of the rotor due to the minute initial imbalance. In most of the cases, however, the motion due to the imbalance will be finite, up to the final lasting balanced position. The second source of the error may be in the vibration. If the rotor vibrates excessively, there is no meaning of measuring such a precision motion, the rotation could simply be attributed to be caused by the vibration.
In conclusion, though, this is not a very difficult experiment and the risk involved in the experiment is very small. The result may come out in the first few weeks if not a few months because it is easy to measure the minute displacement of an object in space using the various methods utilizing interferometer.
The actual force may be calculated by assuming the model universe in which the total mass M is located at the distance r in a form of a thin shell as in the case of Lens-Thirring or by using the simple two mass pole model universe in which the two poles of mass M/2 each are located at the distance r from the center in the opposite directions.
In effect, this experiment measures the total mass and the average distance they are located from us in different kinds of models of the universe.
Calculation Note for the Relativistic Center of Mass Shift from a Solid Hemisphere
Calculation Note 1

In the note, the distance r of the detector from the center of the hemispehre as being equal to R which is the radius of the hemisphere. But this is not correct since the distance from the center of the hemisphere to the poles is half of the radius R.
This correction is reflected in the final estimates of the force.
Tuesday, April 17, 2007
Testable Model Set Up and Preliminary Estimate of the Dipole Gravity Force
In the following, we will calculate the actual dipole gravity force from a rotating 2 meter diameter(1 meter radius) hemisphere made of a solid stainless steel rotating at 100,000 rpm. It may be a relatively large structure and a pretty fast rotating speed. Still it can be considered a manageable set up in a decent sized lab.
From this result, we will have a sense of directions to modify the apparatus to obtain the most desirable effect.
Preliminary calculation shows that for a solid stainless steel hemisphere of radius 1 meter, density 8,000kg/m^3, at 100,000 rpm, at the strongest spot near either side poles of the rotor has the radial gravitational acceleration of 4.54x10^-16 m/sec^2, one side(flat) pulls and the other side(domed) pushes, purely due to dipole gravity.
This is not a very promising level of strength to be considered measurable. It pushes the current technology on earth to the limit. At 1 million rpm, the strength increases to 4.54x10^-14 m/sec^2. The dependency of this force to the radius is 4th power, dependency to the density linear and that to the rpm harmonic(^2).
High density material will certainly increase the level of the strength, but only linearly. Increasing the radius to double will increase the strength to 16 times.
If the radius of the rotor can be increased to 10 times, the acceleration per unit mass on the detector will become 4.54x10^-10 m/sec^2 at 1 million rpm which may be considered still too small.
The size of the rotor in this case is 20 meter in diameter and the rotational speed 1 million rpm. This can hardly be considered a practical experimental set up although it may all depend on the sensitivity of the gravitometer.
Some other method of detection may need to be found.
Relativistic Center of Mass Shift
The following is an illustration of the analytic computation of the shift of the relativistic center of mass in a rotating hemispherical shell.


In the above, rc is the new center of mass that has been shifted by the relativistic mass increase effect, while ro is the original center of mass of the hemisphere when it is at rest. When the rotational speed is slow, which may be the case in a terrestrial experiment, the relativistic shift of the center of mass of a rotating hemisphere becomes
The gravitational dipole moment for this system in a slow rotational speed is given by the mass M times the above delta rc.
This aspect of center of mass shift is obvious in the sense that whoever has the knowledge of special relativity and a little bit of calculus background will be able to figure it out easily. The hardest part would have been to make the connection that it is a very abnormal mechanical system within the boundary of Newtonian mechanics, which may require extensive knowledge of general mechanics. Next hard step would have been to make the connection of this system with general relativity. If one misses any one of these steps or has insufficient knowledge on any of them, it would be next to impossible to get the solution of gravitational dipole moment.
The full article for the details can be found by clicking the link.
Rotational Frequency Dependency of Dipole Gravity






As the rotational frequency increases, the repulsive pole tower potential gets taller, as can be seen in the diagram from the bottom to the top, meaning that the linear trajectory of the jets gets longer as well.
However, it must be noted that the singularity peaks in the diagrams are mathematical artifacts because the height of the tower can not be taller than the height of the monopole at the infinite distance. Because even with that height (that is the same as the monopole at infinity), the jets will stretch to infinite distances. We will introduce a form factor etha to smooth out the singularities so that the potential describes the more realistic picture of the dipole force.
However, the overall qualitative features will not change even if the rotating object becomes a black hole, since it will allow even more faster speed of the rotation and consequently the stronger repulsive force for the linear trajectory.
Monday, April 16, 2007
The Structure of the Jet Formation
The above diagram is derived from the dipole gravity potential expressed below by setting the latitude angle theta equal to zero for the positive Z axis and 180 degree for the negative Z axis, where the form factor etha is introduced to smooth out the sharp singularities which are considered mathematical artifacts.

At the poles of the rotating sphere, the dipole potential indicates the existence of linear trajectories along the rotation axis.
This dipole potential at the poles looks like a funnel if it is viewed in the three dimensional picture. The angular distribution of the potential that produces jets spreads out as the distance increases further away from the center.
From this observaiton, it is expected that particles going into the rotating black hole through the poles of the rotation axis actually have much higher probability of going through a rapid spiraling motion instead of a straight through linear trajectory, which will be the same for the particles coming out.
This picture provides an explanation on why not all the particles going in and out collide each other head on, only to reduce the net stream to zero in a short period of time.
However, the diagram shows clearly that there are possibilities of the matter spilling over from the central harmonic potential region to the side ways when the density of matter exceeds the limit of its capacity within the limited space.
As soon as they cross over the shallow potential hill, there is a deep and powerful fall that pushes them out of the rotation axis.
Also, the observed jets certainly indicates violent collisions of matters along the rotation axis.
If the jets are formed by uniformly outgoing particles only, the observed radiation would be hard to explain.
Note: The longitudinal component of the dipole gravity force in the above diagram needs to be corrected, although the major properites may not be affected, the sign of the force has to be reversed. This issue is discussed in detail in the following "Sign Error in Lens-Thirring Force?" page.
An Isolated Gravitational Dipole Moment

The radial component of the above dipole potential(second term) changes its sign from positive to negative as the latitude angle crosses over the equatorial plane where the latitude angle theta is 90 degree, which means that the gravity force from this dipole moment changes from attractive to repulsive because taking the gradient of the dipole term in the spherical coordinate system will leave the cosine factor untouched.
Do we have antigravity force in our universe?
Can this effect be tested?
I think it depends on the sensitivity of the gravitometer and the physical limitation of the speed of rotation of the giant hemispherical rotor that might be used. The material strength, the density of the material and the nano scale structural imperfection of the rotor in bad combination could result in a devastating catastrophe when the rotational speed gets to a maximum level.
However, one promising feature of this future experiment is that it is controllable.
We don't have to wait for the very precious guest not knowing when and in what dress will he/she make a visit, as it is like in LIGO experiment. Perhaps it may never make a visit and even if it does, we may accidentally miss the opportunity to see it.
All these possible predicaments are not working for LIGO.
How real is this dipole gravity potential?
If there were a super computer which can calculate all the gravity effect generated from the acceleration of each of the mass components within the rotating spherical shell, it would have come up with exactly the same potential derived from the theory of dipole gravity.
How do we know that?
Because the dipole gravity potential matches with the one calculated by analytic method used by Lens-Thirring in the region close to the center of the sphere. The analytic method is not very effective when the term contains singularities as can be seen in the dipole gravity potential. All those deep wells and the high pole towers are the regions typical analytic calculus fails.
Broken Symmetry in General Relativity
So, what is the symmetry breaking in general relativity?
Because of the tradition from Newtonian mechanics that a projectile motion of a macroscopic object can be mathematically described by the motion of the center of mass of the object, spherical object has been favored typically as an ideal sample mechanical system to start with.
The problem with this idealized spherical example was that it hid the important dipole gravity effect in the linearized weak field limit of general relativity.
This can be seen from observing the shift of the center of mass in the two different cases of a rotating hemisphere and a rotating sphere.
The relativistic mass increase effect shifts the center of mass of a rotating hemisphere but not that of a rotating sphere.
Here, we see that the symmetry is broken in relativity in the rotating hemispherical system and that it divulges what has been concealed. It means that a rotating hemisphere has to be dealt with in a totally differently manner in comparison to a rotating spherical system.
The whole basis of the theory of Dipole Gravity is in this symmetry breaking feature of its rotating systems.
In effect, the presence of the shift of the relativistic center of mass is more of a natural and general phenomenon than that of a perfectly carved unnatural spherical system that totally conceals the effect of the shift of the relativistic center of mass.
The fundamental building block of general relativity for a starting model mechanical system is a symmetry broken object like a cone or a hemisphere not a perfect sphere. A rotating sphere can certainly be created by two opposing rotating hemispheres but not the other way around.
Sunday, April 15, 2007
Introduction to Dipole Gravity (Gravito Magnetism)
One of the typical objections to the existence of dipole gravity has been the simple argument that "there is no negative mass in gravitation". But gravity is not electromagnetism. The analogy breaks down fast because there is no apparent magnetic counter part of gravitational phenomena in gravity like in electro-magnetism.
Strangely enough the early quest from the Princeton Wheeler group in gravitation was to look for this magnetic counter part of the gravitation. There are evidences that people considered seriously a rotating donut shaped object to create gravito magnetic effect because this configuration resembles the flow of the mass current in the circular motion as the magnetic effect is created by the electrical current in electromagnetism. All these attempts didn't produce any meaningful results.
However, it is very interesting to note that the formal mathematical expression for the actual dipole gravitational moment in the weak field limit of the linearized theory is rather simple.
The mathematical expression for the gravitational dipole moment simply asks for a displacement of the center of mass of the object in consideration without saying exactly what kind.
Unfortunately, all that has been known about the displacement of an object in physics up to then is either a coordinate translation or by giving it a simple momentum.
Both are physically meaningless because they can be transformed away, in field theoretical term, ie, the phase angle is constant. Moreover, having a displacement of the center of mass of an object without any external force is an unthinkable proposition in Newtonian mechanics because matter simply won't move or jump from one position to the other without a proper cause.
The concept of the relativistic mass increase effect has been known since the theory of special relativity has been published, but the anomalous center of mass shift due to this effect was unknown until Jeong found the system of the rotating hemisphere very peculiar, although it is clear from a moment of thought experiment using a rotating hemispherical object that it does shift the center of mass without a proper cause known in Newtonian Mechanics.
A theory in physics is like a software in modern term, which means the mathematical symbols in the equation mean nothing unless we humans attach the right meaning to it. As is well known in the software science, if one puts in "garbage" data, the software will provide us with "garbage" information. The mathematical equation in physics is very cold and impersonal in that sense. It ignores our stupidity and laughs at us from behind.
This is a quest for the gravito magnetic effect, ie, the dipole gravity.
The quest started by the simple question "what is so special about a rotating hemisphere?" and when it was noticed that a hemisphere shifts its center of mass when in rotation while a rotating sphere doesn't.
What is the cause of this anomaly?
Using the fact that the potential function is a scalar quantity, one can add the potentials from the two opposite hemispheres to construct the full potential for the sphere with the consideration of the fact that their individual centers of mass are located now R/2 from the center of the sphere toward the positive and negative directions of the z axis respectively.
This slight separation(by the distance R) of the two centers of mass of the individual hemispheres within the sphere is the key to this solution because if the two centers of mass were exactly at the same location, this dipole effect would have been canceled out exactly.
The above diagram is the quadrupole gravitational potential for a rotating sphere derived from the theory of dipole gravity. The four poles are aligned along the rotation axis of the rotating spherical shell. This indicates that the rotating sphere forms a static gravitational quadrupole moment, formed by two opposing dipoles, which is not the radiating kind. The total gravity potential(monopole plus dipole) corresponding to the diagram in an analytic form is expressed by,
The two deep potential wells (front and back) indicate the existence of two attractive dipole gravity force centers and also the repulsive ones(represented by the two tall towers ). Particles coming into the attractive dipole potential well along the rotation axis suddenly feels the giant wall of the repulsive potential and they are repelled back to the outside of the ultra compact rotating star, forming two way jet streams of the rotating black holes. It can be noticed that there is a saddle point in between the two repulsive pole towers.
Their fatal mistake was in the fact that they regarded the dynamic mass
increase as being the same as the permanent mass density increase. Later, Cohen speculated intuitively that this force must be due to the quadrupole effect (note the bulging effect of the sphere toward the side) which was a very close observation. Thirring also had the force in the axial direction, which is basically the harmonic oscillator as you can read off from the above graph. Now as we can see these forces are all due to the dipole effect superposed inside a rotating spherical mass shell and the cause for the jets.
As it turns out, Lens-Thirring force is a small local feature out of the many diverse features of dipole gravity ranging from zero to infinite distances and the full angular variations.
The potential also shows the dips around the equatorial plane, meaning that there is non zero contribution of dipole gravity force around the equatorial plane of the rotating stars. It also indicates that satellites tend to align to the equatorial plane because of the angular dependencies of dipole gravity.
It will be interesting to see if this potential will be able to account for most of the dark matter problems or will there still be missing matter problem even after this inclusion in the numerical computation and the curve fitting study.
In a recently published paper(2007), jets have been observed from a rotating neutron star. So, the black hole and the generally assumed associated complex mechanism must not be the absolute requirement for jets to form in the rotating ultra compact stellar objects.
Any ultra compact stellar object with high speed of angular momentum is capable of generating jets on its axis according to the theory of gravito magnetism(dipole gravity).
Note: The diagram has been fixed to make the potential to match with Lens-Thirring force. It is noted that the repulsive nature of the radial component of the dipole gravity force in the diagram is not consistent with the dark matter problem. This issue is discussed in detail in the "Sign Error in Lens-Thirring Force?" page.
Welcome to Dipole Gravity forum
This is a discussion forum for Dipole Gravity also called Dipole Antigravity or Gravito Magnetism. It is the same physical effect which has many different names and faces. We welcome postings from physics graduate students, physics professionals, who have in depth knowledge on the subject of Gravitation, general relativity and cosmology in general. No spams, no profanity allowed. We want this forum to be very focused and professional. If you don't have proper background on the related topics, please try to be a guest member instead of being a contributor.
The general guideline for posters is to remain anonymous. Unless poster specifically wants to let others know his/her affiliation, it will be fine. But it is neither recommended nor discouraged.
The abstract of the published paper can be downloaded from the journal Physica Scripta http://www.iop.org/EJ/search/1402-4896/1 and type eue jin jeong in the author search.
Or to purchase the full article directly from the journal web site, go to,
http://www.iop.org/EJ/article/-search=18866999.1/1402-4896/59/5/002/physscr_59_5_002.pdf
and follow the instructions.
Or download the llnl.gov archive version from
http://www.tachyonics.com/isol.pdf
The basic contents of the papers are the same. We will make the journal version available to qualified members upon request by email.
For private communication, please send email to ejeong1@sbcglobal.net.


